Programming Carcassonne

Code: https://github.com/wingedsheep/carcassonne

This year I decided to quit doing gigantic projects that I never finish, and instead focus on smaller projects that can be completed in a few weeks. The goal is to get better at machine learning, especially reinforcement learning. I want to understand the shortcomings of the current methods so that I can think about improvements and contribute to the field. The first step in this process is to create an interesting environment for testing algorithms. At the same time I want to learn how to program in Python, since this is the most used language for machine learning.

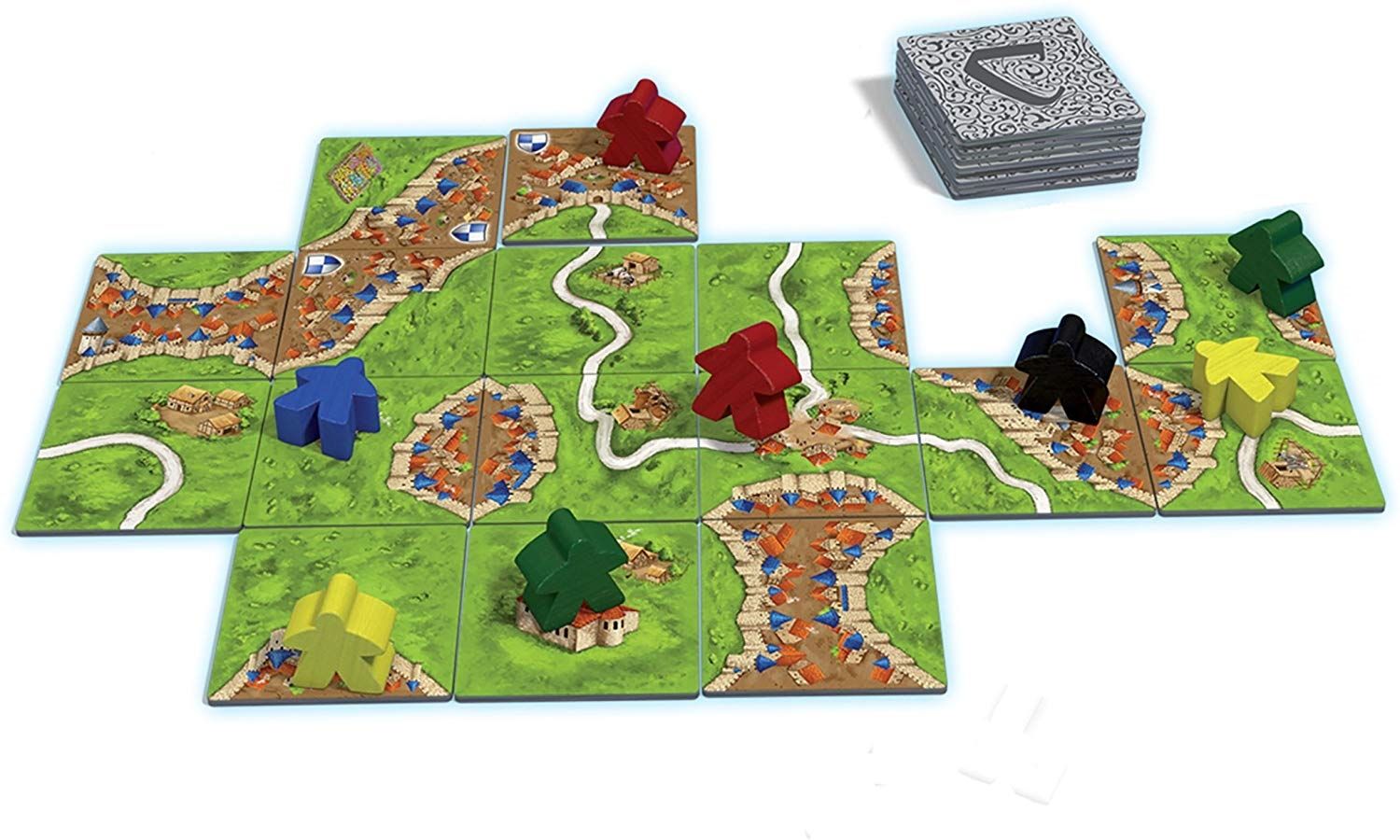
Recently I have been playing lots of Carcassonne games. A board game in which you take turns laying tiles with cities, roads and fields. You slowly build a world and in the meantime accumulate points by claiming parts of that world.

These are the reasons Carcassonne looks like an interesting reinforcement learning environment to me:

• There are multiple players (agents) playing the game
• Scoring is a combination of short term and long term rewards
• The challenge of representing this game as a reinforcement learning problem
• Imperfect information

Rules of the game

The players alternate turns. In the base game both start with 7 meeples.

At the beginning of each players' turn they take a tile from a closed stack.
A tile can be rotated and placed anywhere on the board if all the edges of the tile match the edges of connecting tiles. Except for the first tile played, tiles always need to have at least one connected tile. If it is impossible to play a tile it is discarded and a new tile is drawn from the stack.

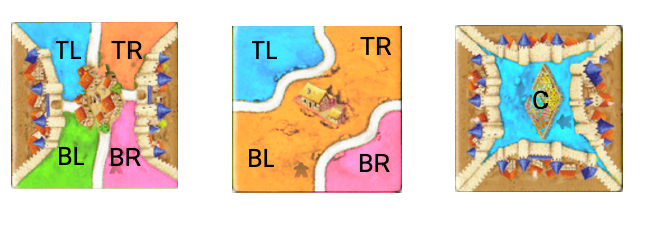
Say the following 3 tiles are on the board and you draw the one in orange.

The new tile can only be placed in the empty spot after rotating it, since it needs to match the road on the top side and the city on the left.

In the second part of a players' turn they can play a meeple. A meeple is a wooden figure you can put on the tiles. A player can use their meeples to score points.

A player can choose to place one of their meeples on the tile they just put on the board. A meeple can be placed on:

• A city, if none of the connected cities already contain a meeple
• A road, if none of the connected roads already contain a meeple
• A chapel
• If playing with the additional rule for farmers a meeple can also be placed on a field, if none of the connected fields already contain a meeple

Points are scored as follows:

• city: A city is finished if it has no more unconnected edges. The meeples are removed and the player with the most meeples on this city gets 2 points for every city tile, or 4 points if the tile has a shield icon. If the city is unfinished by the end of the game the player with most meeples gets half the points.
• road:  A road is finished if it has no more unconnected edges. the player with the most meeples on this road gets 1 point for every road tile. If the city is unfinished by the end of the game the player with most meeples still gets 1 point for every tile.
• chapels or flowers: A chapel or field of flowers is finished if it is surrounded by tiles on all sides, meaning that there are 8 tiles surrounding the tile with the chapel. Finished or unfinished, the player with a meeple on the chapel gets 1 point for every tile surrounding the tile, plus one point for the tile itself.
• fields: A player can place a farmer on a field. Fields are connected in the same way as cities. At the end of the game players get 3 points for every city connected to a field.

Game API  

The code for this project can be found on https://github.com/wingedsheep/carcassonne

Before I started programming I thought of how users of the code would interact with it. How it could be most useful in other projects, and my future machine learning project. I got most of my inspiration from the way environments are defined in OpenAI gym. (https://gym.openai.com/)

The API has the following functions:

• reset: Reset the game to an initial state, with randomly shuffled tiles
• step(player, action): Update the game state by executing an action for the given player.
• render: Render the current game state
• is_finished: true if the game is finished, false otherwise
• get_current_player: Return the player who currently has to make a move
• get_possible_actions: Return all possible actions

This is an example of playing out a random game using the API.

import random  
from typing import Optional  
  
from wingedsheep.carcassonne.carcassonne_game import CarcassonneGame  
from wingedsheep.carcassonne.carcassonne_game_state import CarcassonneGameState  
from wingedsheep.carcassonne.objects.actions.action import Action  
from wingedsheep.carcassonne.tile_sets.supplementary_rules import SupplementaryRule  
from wingedsheep.carcassonne.tile_sets.tile_sets import TileSet  
   
game = CarcassonneGame(  
	players=2,  
	tile_sets=[TileSet.BASE, TileSet.THE_RIVER, TileSet.INNS_AND_CATHEDRALS],  
	supplementary_rules=[SupplementaryRule.ABBOTS, SupplementaryRule.FARMERS]  
)  
  
while not game.is_finished():  
    player: int = game.get_current_player()  
    valid_actions: [Action] = game.get_possible_actions()  
    action: Optional[Action] = random.choice(valid_actions)  
    if action is not None:  
        game.step(player, action)  
    game.render() 

First a game object is created.  This creates a new game instance using the given configuration. This configuration includes the number of players, the tile sets (Carcassonne expansions) and supplementary rules that are used.

Next, the game is played out by getting all valid actions from the API and randomly selecting one each turn until the game is finished.

So now we know what the goal is. To create a flexible API that allows developers to quickly set up a Carcassonne game.

How to get started? What do we need?

• We have the definition of the API, i.e. how developers should be able to interact with the code.
• How to describe and initialize the game?
• How to describe tiles in an elegant way?
• How to get from one game state to another using actions?
• How to describe projects (cities, roads, chapels) that involve multiple tiles, and how to see if they are finished?
• How to calculate score?
• What are the next steps once the API is finished?  

Game state

A game state consists of all the information that is needed to describe the current state of the game. In the game state is the following information:

• The tiles left to draw
• The tile that has to be playe
• The board, i.e. which tiles the players have already played and which meeples are on the board
• The number of players and the current player
• The number and types of meeples left for every player
• The score for every player
• The game phase (playing tiles or playing meeples)

When starting a game a new board is created. For simplicity we can say that the board has a fixed size. It rarely happens that a Carcassonne game grows outside the bounds of a 30x30 board.

We initialize the board as a 2d array with rows and columns. Every coordinate (row and column combination) contains an optional Tile. This means it can be filled either with a None object or a Tile object.

board_size = (30, 30) 

self.board: [[Optional[Tile]]] = [[None for column in range(board_size[1])] for row in range(board_size[0])]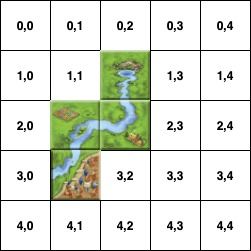

After the board is initialized the tiles are randomly placed in a stack. If the river expansion is included this step is a bit different, since all the river tiles have to be played first. When playing the game, the first tile from the deck is popped every time a player plays a tile.

The expansions are defined as TileSets. Every TileSet has a collections of tiles. Every tile has a definition, and a count. The definition describes all properties of the tile and the count describes how many of them are in the TileSet.

def initialize_deck(self, tile_sets: [TileSet]):
   deck: [Tile] = []

   # The river
   if TileSet.THE_RIVER in tile_sets:
       deck.append(the_river_tiles["river_start"])

       new_tiles = []
       for card_name, count in the_river_tile_counts.items():
           if card_name == "river_start":
               continue
           if card_name == "river_end":
               continue

           for i in range(count):
               new_tiles.append(the_river_tiles[card_name])

       random.shuffle(new_tiles)
       for tile in new_tiles:
           deck.append(tile)

       deck.append(the_river_tiles["river_end"])

   new_tiles = []

   if TileSet.BASE in tile_sets:
       for card_name, count in base_tile_counts.items():
           for i in range(count):
               new_tiles.append(base_tiles[card_name])

   if TileSet.INNS_AND_CATHEDRALS in tile_sets:
       for card_name, count in inns_and_cathedrals_tile_counts.items():
           for i in range(count):
               new_tiles.append(inns_and_cathedrals_tiles[card_name])

   random.shuffle(new_tiles)
   for tile in new_tiles:
       deck.append(tile)

   return deck

So now we can initialize a game, but we still have to be able to describe the different parts of the game.

Tiles

Perhaps the most important part of the game are the tiles. At the beginning of each turn a player has to play a tile to create a landscape. All the tiles have different properties that need to be described elegantly.

The properties of a Tile include:

• Roads
• Cities
• Rivers
• Fields (grass)
• If it has a shield icon (gives extra points for cities)
• Chapel
• Flowers (Abbots can be placed on flowers)
• Inn (gives extra points to roads, but negates all the points if the road is not finished)
• Cathedral (gives extra points to cities, but negates all the points if the city is not finished)
• Image (how does the tile look)

Cities

For cities on a tile we have to know two things:

• Which cities on the tile are connected?
• Which sides of the tile have cities on them?

Just indicating which sides of a tile have a city on them is enough to decide where a player is allowed to place a tile, but not enough for calculating which cities are connected. We need to be able to describe the difference between the following two tiles.

If we would describe the tiles as a collection of city sides, the representation for both tiles would be the same.

cities_a = [TOP, LEFT]
cities_b = [TOP, LEFT] 

Connected city groups are needed to distinguish between the two. The representation becomes a collection of city groups, where a city group is a collection of sides. If cities on a tile are connected they belong to one city group.

cities_a = [
	[TOP],
    [LEFT]
]

cities_b = [
	[TOP, LEFT]
]

Roads

Roads have the same property as cities. We need to know which sides of the tile are connected by road and which sides have a road on them.

The difference between the following two roads, which have similar sides that contain a road, can be represented as follows.

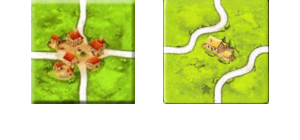
roads_a = [
	[TOP, CENTER],
    [RIGHT, CENTER],
    [BOTTOM, CENTER],
    [LEFT, CENTER]
]

roads_b = [
	[TOP, LEFT], 
    [BOTTOM, RIGHT]
]

With this representation we can also see that the roads for tile A all end on this tile, while the roads for tile B can connect two other tiles.

Rivers

Can be represented the same as roads.

Fields

The representation of fields is a bit more complex, since they can be split by roads, rivers and cities. Four sides to represent all options is no longer enough. We need 8 sides for this.

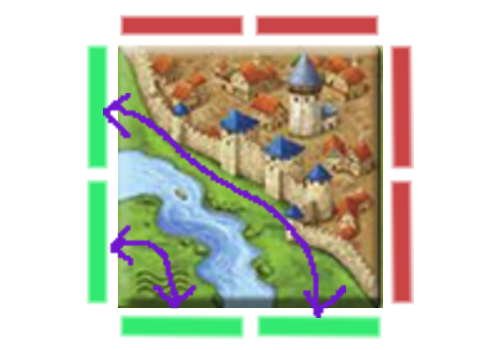
For this tile we can see that the "top left left" is connected to the "bottom right bottom" and the "bottom left left" is connected to the "bottom left bottom". The fields on this tile can be represented as follows:

fields = [
	[TOP_LEFT_LEFT, BOTTOM_RIGHT_BOTTOM], 
    [BOTTOM_LEFT_LEFT, BOTTOM_LEFT_BOTTOM]
]

Actions

Actions are the means to get from one game state to another. Performing an action in one game state leads to another game state. The API can return a list of all actions that are allowed. How do we determine which actions are allowed?

A players' turn is divided in two phases: the tile phase and the meeple phase.
In the tile phase the player can alter the board by adding tiles to it. In the meeple phase the player can alter the board by placing meeples on the last played tile.

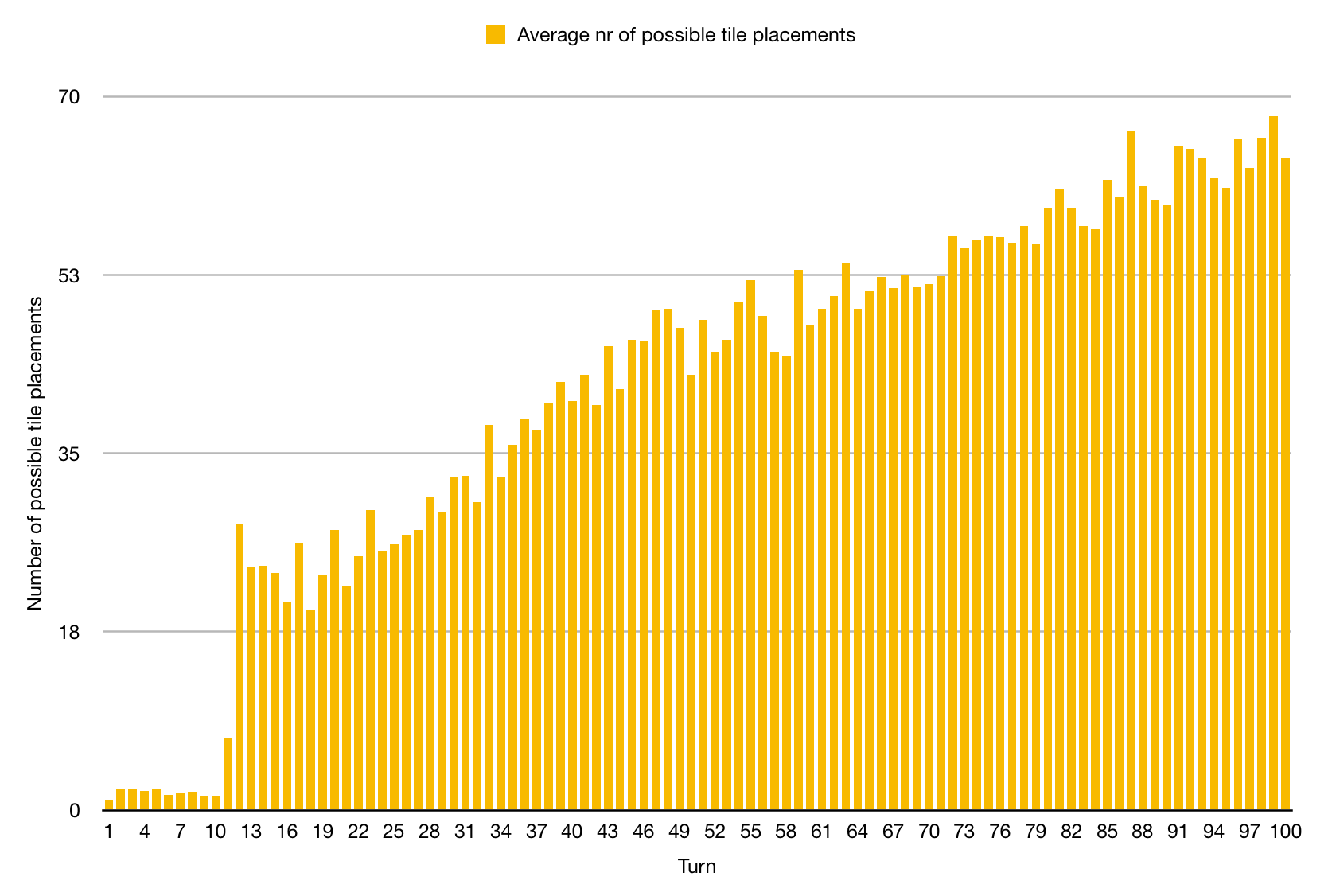
Number of possible moves

We took the average number of possible tile placements through 10 random games with 2 players using the expansions "The river" and "Inns and cathedrals". These are the results. In the beginning the number of moves is low, because players can only play river tiles. Near the end the average number of possible moves grows to almost 70. Also, an average random game with two players lasts for around 100 turns.

Tile phase

First a random tile is drawn that has to be placed somewhere on the board.
We can find out all the locations where the current tile can be placed by checking all the rotations of the tile against all the coordinates on the board. A tile can be placed if all four sides either match the terrain type (city, river, road, fields) of the adjacent tile, or if there is no adjacent tile. Except for the first tile, every tile needs to have at least one adjacent tile.

tile_to_play = game_state.get_tile_to_play()

allowed_actions = []

# board is a 2d array containing Tile objects.
# We iterate through all the rows and columns
for row_index, board_row in enumerate(game_state.board):
	for column_index, column_tile in enumerate(board_row):
    
    	# Not allowed if there is already a tile in this spot
    	if column_tile is not None:
        	continue
            
        # Check all possible orientations of the new tile
        for rotations in range(0, 4):
        
        	rotated_tile = current_tile.turn(rotations)
        	
            # Collect the surrounding tiles
            # None if there is no tile or outside of board bounds
        	top = game_state.get_tile(row_index - 1, column_index)
        	bottom = game_state.get_tile(row_index + 1, column_index)
        	left = game_state.get_tile(row_index, column_index - 1)
        	right = game_state.get_tile(row_index, column_index + 1)
            
            if top is None and right is None and bottom is None and left is None: 
            	continue
            
            fits = True
            for side in [TOP, RIGHT, BOTTOM, LEFT]:
            	terrain_type = tile.get_terrain_type(side)
                
                if side == TOP: 
                	fits_top = top is None or \
                    	top.get_terrain_type(BOTTOM) == terrain_type
                    fits = fits and fits_top
                elif side == RIGHT:
                	fits_right = right is None or \
                    	right.get_terrain_type(LEFT) == terrain_type
                 	fits = fits and fits_right
                elif side == BOTTOM:
                	fits_bottom = bottom is None or \
                    	bottom.get_terrain_type(TOP) == terrain_type
                    fits = fits and fits_bottom
                else:
                	fits_left = left is None or \
                    	left.get_terrain_type(RIGHT) == terrain_type
                    fits = fits and fits_left
                    
            if fits:
            	allowed_actions.add(Action(rotated_tile, row, column))
                        
return allowed_actions

If the game is played with the river expansion there is an additional rule for fitting river tiles. In the river expansion players create a connected river first, that serves as a starting point for the rest of the board. To make sure players can always finish the river it is not allowed to place two river tiles that make a turn in the same rotational direction (clockwise, counterclockwise). If a player plays a clockwise turn, the next turn has to be counterclockwise.

This is done by saving the last played rotational direction in the game state. If the newly placed tile has the same rotational direction, the action is not allowed.

Meeple phase

The next phase of the game is the meeple phase. Players can choose to take one of their meeples (if they have any) and put them somewhere on the tile they just placed on the board.

There are 5 possible positions to place a meeple, and another 5 possible positions to place a farmer meeple.

The 5 possibilities for placing a meeple on a normal tile are: top, right, bottom, left and center. The four sides are used for cities and roads. The center is only used for chapels and flowers.

The 5 possibilities for placing a farmer are top left, top right, bottom left, bottom right and center. But center is only necessary for tiles without any outgoing connections to other tiles.

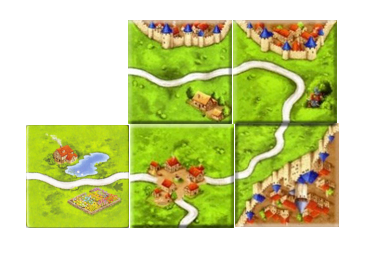
A meeple can only be placed on a spot if there are no meeples on connected cities / roads or fields. In the example below, after placing the tile on the left, the yellow player is not allowed to put their meeple on the city on the right side of the tile, since this city is connected to another city with a green meeple on it. The yellow player is allowed to play their meeple on the top side city, since this city is not connected yet.

To see whether we are allowed to place a meeple somewhere we need an algorithm to find connections to other tiles.

The pseudocode for finding all connected sides of a city. The same code can be applied to roads and fields. But for fields we have to take into account that instead of 4 sides they have 8.

def find_city(game_state, coordinate, side):
	tile = game_state.get_tile(coordinate)
    
    connected = find_connected_sides(game_state, coordinate, side)
    unexplored = find_adjacent_sides(game_state, connected)
    ignored = Set()
            
    # Continue while there are unexplored edges
    while len(unexplored) != 0:
    	to_explore = unexplored(pop)
        
        # If there is no tile on this side, add it to ignored, 
        # to prevent visiting it again.
        new_tile = game_state.get_tile(unexplored.coordinate)
        if new_tile is None: 
        	ignored.add(to_explore)
        
        new_connected = find_connected_sides(
        	game_state, 
            to_explore.coordinate,
            to_explore.side
        )
        connected = connected.union(new_connected)
        new_unexplored = find_adjacent_sides(new_connected)
        for new_to_explore in new_unexplored:
        	if not (new_to_explore in connected or new_to_expore in unexplored or \ 
            		new_to_explore in ignored):
            	unexplored.add(new_to_expore)
                
    return connected 
    
def find_connected_sides(game_state, coordinate, side):
	# Find the connected sides on the tile
    # Remember cities for a tile is described as a list of lists of connected sides
    for connected_sides in tile.cities:
    	if side in connected_sides:
        	return set(
            	map (
                	lambda side: CoordinateWithSide(coordinate, side),
                    connected_sides
                )
            )
    
    # Return an empty set if there is no city on this side of the tile
    return Set()
    
def find_adjacent_sides(game_state, coordinates_with_side):
	return set(
		map (
			lambda coordinate_with_side: adjacent(coordinate_with_side),
			coordinates_with_side
        )
    )
    
def adjacent(coordinate_with_side): 
	if side == TOP:
    	return CoordinateWithSide(
        	Coordinate(coordinate.row - 1, coordinate.column), 
            BOTTOM
        )
    elif side == RIGHT:
    	return CoordinateWithSide(
        	Coordinate(coordinate.row, coordinate.column + 1), 
            LEFT
        )
    elif side == BOTTOM:
    	return CoordinateWithSide(
        	Coordinate(coordinate.row + 1, coordinate.column), 
            TOP
        )
    else:
    	return CoordinateWithSide(
        	Coordinate(coordinate.row, coordinate.column - 1), 
            RIGHT
        )
    

Score

Every turn, after the meeple phase, we check if the placed tile finishes any cities, roads or chapels. This is done after the meeple phase because players are allowed to still place a meeple on a finished city, road or chapel before the scores are counted. For every side of the city we check what the terrain type is, and if the new tile completed anything.

If a city or a road gets completed we check all it's positions for placed meeples. It is possible that one city or road has multiple meeples on it. The player with most meeples gets the points. After the scores are added all meeples get removed from the finished project and can be used again.

At the end of the game scores for unfinished projects are counted. This is done by looping through the placed meeples, finding the project corresponding to their location (city, road, chapel, field) and finding out how many other meeples are on the same project. The player with most meeples on the project wins and all meeples get removed. This process continues until there are no more placed meeples remaining.

Preparation for reinforcement learning

The initial thought behind this project was to create an interesting reinforcement learning environment to be able to try out different algorithms.

For this to be feasible the project needs two more things:

• Game state and action space need to be represented in a way that can serve as input and output of a neural network
• It needs to be fast. Reinforcement learning algorithms such as AlphaZero play many games (44.000.000 games of chess were played in 4 hours by AlphaZero)

A good way to prepare the game for reinforcement learning would be to try to get it in a framework like OpenAI gym or the recently released DeepMind ACME.

For converting the game state to a matrix I'm looking at the representation of chess in the AlphaZero paper. They encode the game state as a matrix, where every plane in the matrix encodes one specific property. For Carcassonne the following properties of the game state should be encoded:

• Tiles with their properties
• Spatial relations between tiles. Adjacent tiles can influence each other
• The current tile to play
• Number of remaining tiles
• The positions of the meeples on the board
• Playable meeple counts

Properties of an action that should be encoded:

• Action type: Are you playing a tile or a meeple?
• The coordinate of the action
• Rotation (if a tile is being played)
• Type of meeple: normal, farmer, abbot, big meeple
• Option for not playing anything (if allowed)

My first thought for encoding the board in a matrix is as follows. There is a plane in a matrix that encodes a single property. For example: "Is there a road connection between the left and right for this tile", if so encode a 1, otherwise a 0.

A matrix for roads from left to right could look as follows:

[[0, 1, 0]
 [1, 0, 0]]

[[0, 1, 1]
 [0, 0, 0]]

[[0, 1, 1]
 [1, 1, 0]]

Any property of the board can be encoded in such a plane. All property planes stacked on top of each other would be the state matrix.

There would have to be the following number of planes (using expansions "the river" and "inns and cathedrals")

• Cities: 10 planes
• Roads: 10 planes
• Rivers: 10 planes
• Fields: 36 planes
• Special properties: 4 planes (chapel, flowers, shield, cathedral)
• Inns: 4
• Meeples: 5 x the number of players
• Abbots: the number of players
• Farmers: 5 x the number of players
• Big farmers: 5 x the number of players
• Big meeples: 5 x the number of players
• One extra plane to encode extra properties like: The current tile, remaining meeples per player, scores, remaining tiles

So for a game with a board size of 30 x 30 and 2 players you would get a state space of 30 x 30 x 117. A total number of 105.300 input parameters.

An action could be encoded as a vector:

• Action type: 3 (tile, play meeple, remove meeple (only for abbots) or pass)
• Board row to perform action on: board size
• Board column to perform action on: board size
• Tile rotation: 4 (if action is a tile action)
• Meeple position: 9 (9 possible meeple positions on a tile)
• Meeple type: 5 (meeple, big meeple, abbot, farmer, big farmer)

So for a game with a board size of 30 x 30 and 2 players you would get an action vector of length 81. Or if we have an output neuron for every possible action we would have 486.000 output neurons. I'm not sure yet how to properly put this large action space in an algorithm.

So what is the next step?

Before starting on a reinforcement learning algorithm to play Carcassonne I want to understand the algorithms better by applying them to a simple environment first. The first algorithms I want to understand better are AlphaZero and MuZero. Once I implemented those myself and understand them better, it is time to apply them to Carcassonne!